Чтобы лучше понимать представленный материал, рекомендую обратиться к предыдущим заметкам по теме:
При игре в тетрис вам доступно не так много действий. Вы можете двигать активный элемент по игровому полю влево-вправо, а также вращать его против часовой стрелки. Кроме того, элемент находится в состоянии падения, которое вы можете ускорить. Последовательно разберем каждое из этих возможных изменений.
По правилам игры движение элемента в горизонтальном направлении возможно только на один блок влево или вправо (точно по сетке).
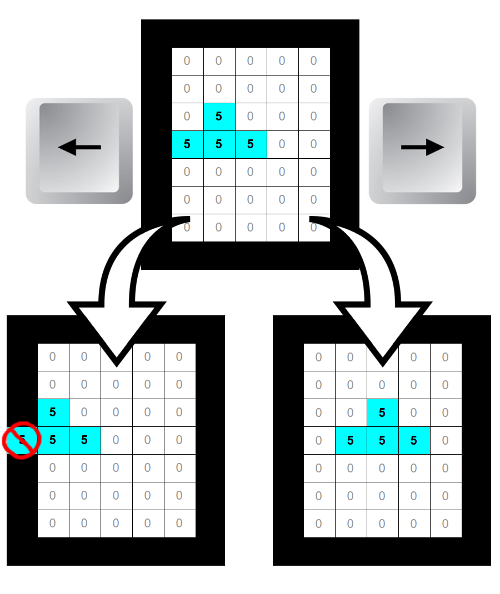
Для выполнения сдвига достаточно изменить x-координату элемента:
item.setPosition(
item.getXPoints() + offsetPoints,
item.getYPoints()
);
Значение offsetPoints по модулю должно быть равно количеству точек в блоке. Для движения влево используется отрицательное значение, а для движения вправо - положительное.
Однако этот код не учитывает одну неприятность: активный элемент может двигаться по полю без каких либо ограничений, или даже уйти за его границы.
Чтобы решить эту проблему, в прошлый раз мы реализовали функцию hasCollisions(), которая умеет обнаруживать столкновения между активным элементом и блоками игрового поля.
Если считать, что в результате движения влево или вправо элемент должен остаться в корректном состоянии, а корректное состояние означает, что элемент находится в свободных блоках игрового поля (не имеет столкновений), то алгоритм сводится к простой проверке, которая записывается с помощью следующего кода:
void TetrisModel::moveItemLeft() {
moveItemX( -BLOCK_SIZE );
}
void TetrisModel::moveItemRight() {
moveItemX( BLOCK_SIZE );
}
void TetrisModel::moveItemX( int offsetPoints ) {
TetrisItem item = m_activeItem;
// Пробуем сдвинуть копию элемента
item.setPosition( item.getXPoints() + offsetPoints, item.getYPoints() );
if( !hasCollisions( item ) ) {
// Если столкновений нет (состояние корректное), то принимаем это состояние
m_activeItem = item;
}
// Иначе сдвиг запрещен и состояние теряется, а исходный элемент остается на месте
}
Логика вращения элемента строится на том же принципе, что и движение влево-вправо: если состояние элемента после вращения остается корректным (столкновения отсутствуют), то принимаем это состояние, иначе ничего не делаем.
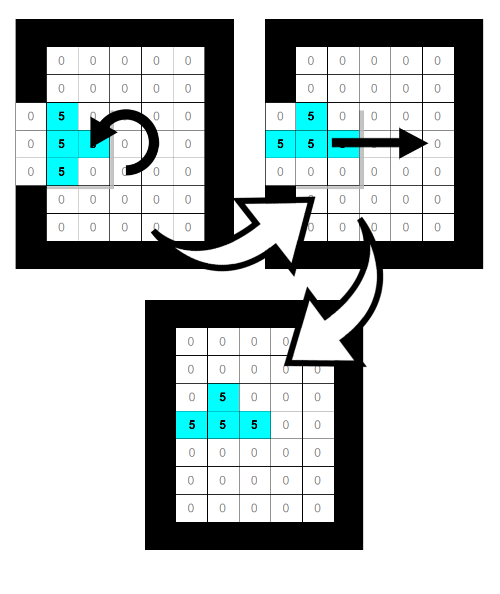
На C++ это можно записать следующим образом:
void TetrisModel::rotateItem() {
TetrisItem item = m_activeItem;
item.rotate();
if( !hasCollisions( item ) ) {
m_activeItem = item;
}
}
Функция-член rotate() класса TetrisItem реализована довольно просто, поскольку сделано предположение, что внутренняя матрица элемента должна быть квадратной:
void TetrisItem::rotate() {
Matrix rotatedMatrix( getSizeBlocks() );
for( int i = 0; i < getSizeBlocks(); ++i ) {
rotatedMatrix[ i ].resize(
getSizeBlocks()
);
for( int j = 0; j < getSizeBlocks(); ++j ) {
rotatedMatrix[ i ][ j ] =
m_matrix[ j ][ getSizeBlocks() - 1 - i ];
}
}
m_matrix = rotatedMatrix;
}
Более сложную версию подобной функции мы разбирали, когда говорили о разработке через тестирование в Qt.
Однако мы еще не закончили с вращением. Поскольку элементы тетриса имеют разную форму, то большинство из них не вписываются ровно в квадрат (по матрице). Это означает, что если после вращения элемент окажется в некорректном состоянии, то возможно два варианта:
Дополним реализацию функции rotateItem() в соответствии со вторым вариантом:
void TetrisModel::rotateItem() {
TetrisItem item = m_activeItem;
item.rotate();
if( !hasCollisions( item ) ) {
m_activeItem = item;
return;
}
// Пробуем сдвинуть на один блок вправо
item.setPosition( item.getXPoints() + BLOCK_SIZE, item.getYPoints() );
if( !hasCollisions( item ) ) {
m_activeItem = item;
return;
}
// Пробуем сдвинуть на один блок влево (относительно исходной позиции)
item.setPosition( item.getXPoints() - blocksToPoints( 2 ), item.getYPoints() );
if( !hasCollisions( item ) ) {
m_activeItem = item;
return;
}
}
Движение активного элемента по вертикали немного сложнее, чем движение по горизонтали. Это связано с тем, что перемещение происходит не по сетке.
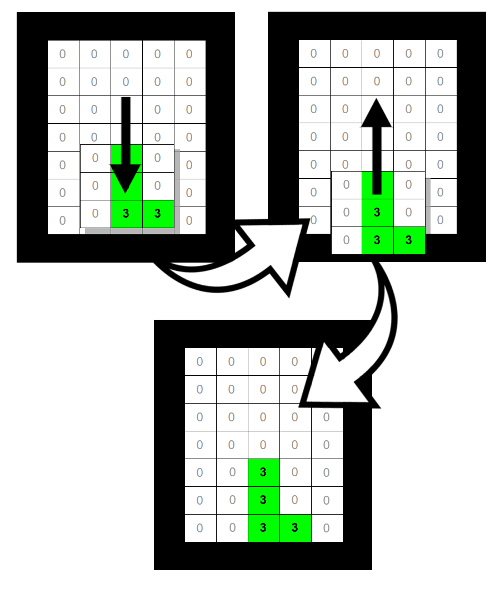
Однако начать реализацию можно так же:
void TetrisModel::doStep() {
TetrisItem item = m_activeItem;
item.setPosition(
m_activeItem.getXPoints(),
m_activeItem.getYPoints() + m_speed
);
if( !hasCollisions( item ) ) {
m_activeItem = item;
}
}
Обратите внимание, что doStep() будет вызываться Контроллером автоматически через заданные временные интервалы. При этом скорость падения элемента определяется переменной m_speed (измеряется в точках за шаг).
Недостаток этой реализации заключается в том, что она не работает :)
Действительно, в зависимости от скорости элемент может просто зависнуть над дном игрового поля или занятыми блоками. Это произойдет, если расстояние между ними окажется меньше значения скорости.
Исправить проблему довольно легко. Воспользуемся тем же способом, который использовали в случае поворота: начнем выталкивать активный элемент вверх, пока он не окажется в корректном состоянии:
void TetrisModel::doStep() {
TetrisItem item = m_activeItem;
item.setPosition( m_activeItem.getXPoints(), m_activeItem.getYPoints() + m_speed );
if( !hasCollisions( item ) ) {
m_activeItem = item;
} else {
while( hasCollisions( item ) ) {
item.setPosition( item.getXPoints(), item.getYPoints() - 1 );
}
m_activeItem = item;
}
}
Следует учитывать, что этот алгоритм будет работать не самым лучшим образом, когда блок состоит из большого числа точек. Однако при необходимости его не так сложно усовершенствовать.
На этом мы завершаем анализ игровой механики тетриса. Можно считать, что движок готов. Однако игры у нас до сих пор еще нет, поскольку в любой игре должны быть правила. В следующий раз мы займемся реализацией именно этого аспекта игры тетрис (см. реализация соблюдения правил тетриса)…